Source (restricted to non-HBO-Max regions)

Kamala Harris is known to love Venn diagrams and would be cringing hard at this.

For reference, circles in Venn (Euler) diagrams are sets of objects with a certain property. Select objects are shown inside or outside of each circle depending on whether they belong to the set.
A good example is xkcd 2962:
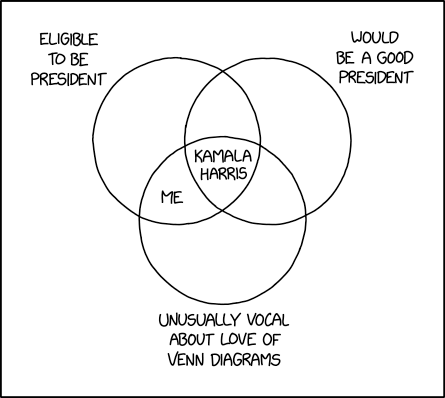
Hard to imagine political rhetoric more microtargeted at me than 'I love Venn diagrams. I really do, I love Venn diagrams. It's just something about those three circles.'

    • ChaoticNeutralCzech@feddit.orgOPEnglish
      1·
      5 days ago

      If he was a mathematician with an audience of mathematicians that all knew this was wrong, the error could have worked as an extra intentional joke. However, the joke he went for could have been made without this error.

      Basically, this is an unforced mistake that ruined a joke for some while having little to no effect on others’ enjoyment of it. You’re in the latter group and I recognize there is a significant number of you in JO’s live audience as well as on Lemmy, as this post is quite controversial.

  • bobzilla@lemmy.worldEnglish
    0·
    6 months ago

    Can someone explain what part he’s incorrect about? (Since we’re in ConfidentlyIncorrect)

          • tobogganablaze@lemmus.orgEnglish
            0·
            6 months ago

            You have two strings and in the overlap you have the concatenated string formed from the parts. Again, not useful but a totally valid interpretation.

            So … can you actually explain why you think it is incorrect or is snarky comments all you got?

            • ChaoticNeutralCzech@feddit.orgOPEnglish
              1·
              6 months ago

              That picture does not make it clear that the labels refer to regions, not elements. A clearer explanation of set operators is the following:

              Set worksheet

              1. B (Set B)
              2. A ∪ B (Union of A and B)
              3. A (Set A)
              4. A \ B (A minus B; notation varies)
              5. B \ A (B minus A)
              6. A ∩ B (Intersection of A and B)