

Ha ha, maybe. The article is pretty short. However, the actual paper linked at the bottom of the article is titled “Hamiltonian cycles on Ammann-Beenker Tilings” (unfortunately I can only see the abstract), so the original authors are also responsible!
It’s my thinking that the key point of thr Hamiltonian cycle in this context is it visits nodes only once thereby creating a unique path. The trick here seems to be then joining those paths for a collection of subgraphs? I’m really not sure. It’s a bit beyond me, but I find it interesting to think about.




















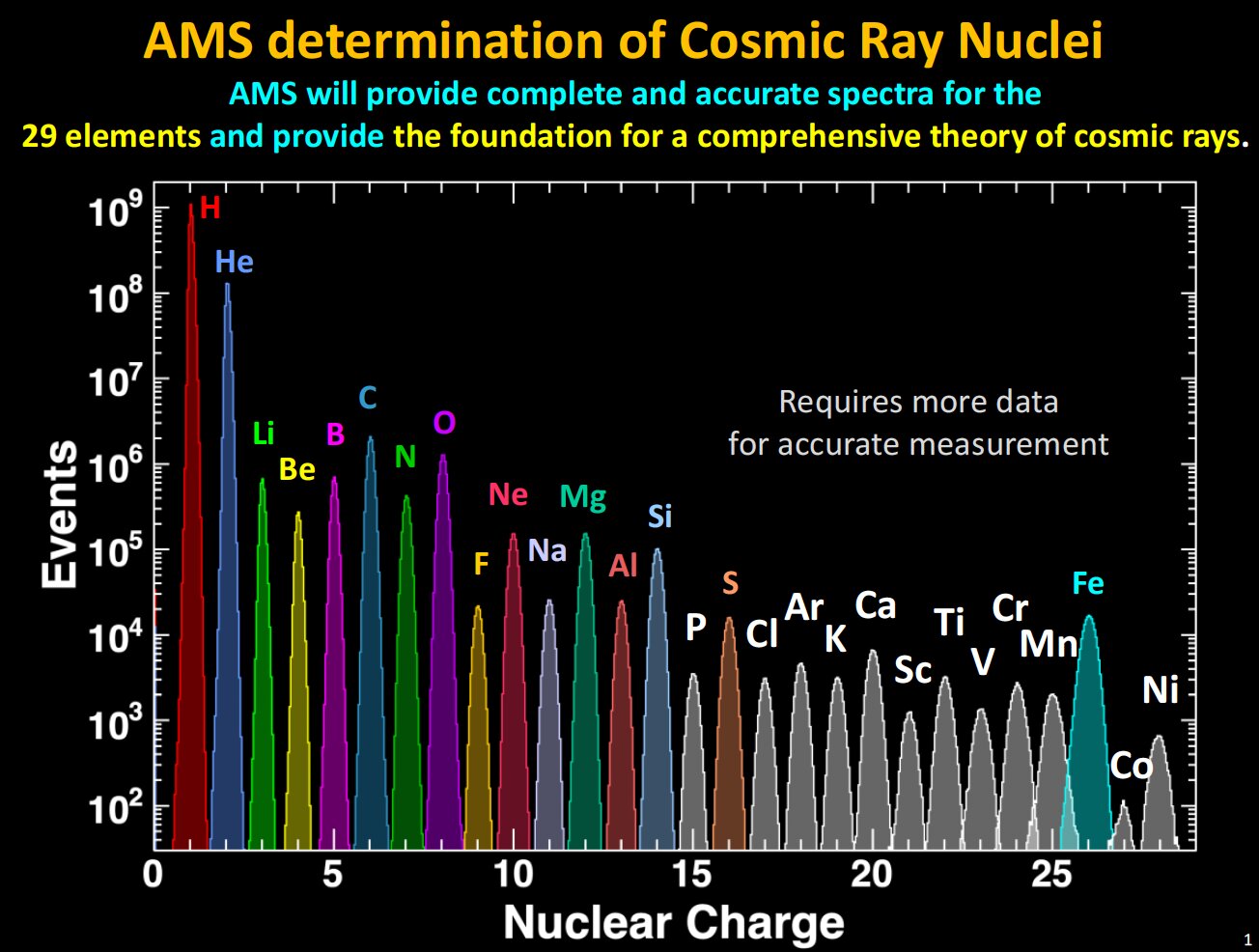



Here is the novelization of the cartoon… sort of. As She Climbed Across the Table by Jonathan Lethem.